The Unit Circle Table – Your Key to Understanding Trigonometry

Ever found yourself staring at a trigonometric equation, feeling lost in a sea of sines and cosines? You’re not alone! Mastering trigonometry can be daunting, but there’s a powerful tool that can help simplify the process and unlock a deeper understanding: the unit circle table.

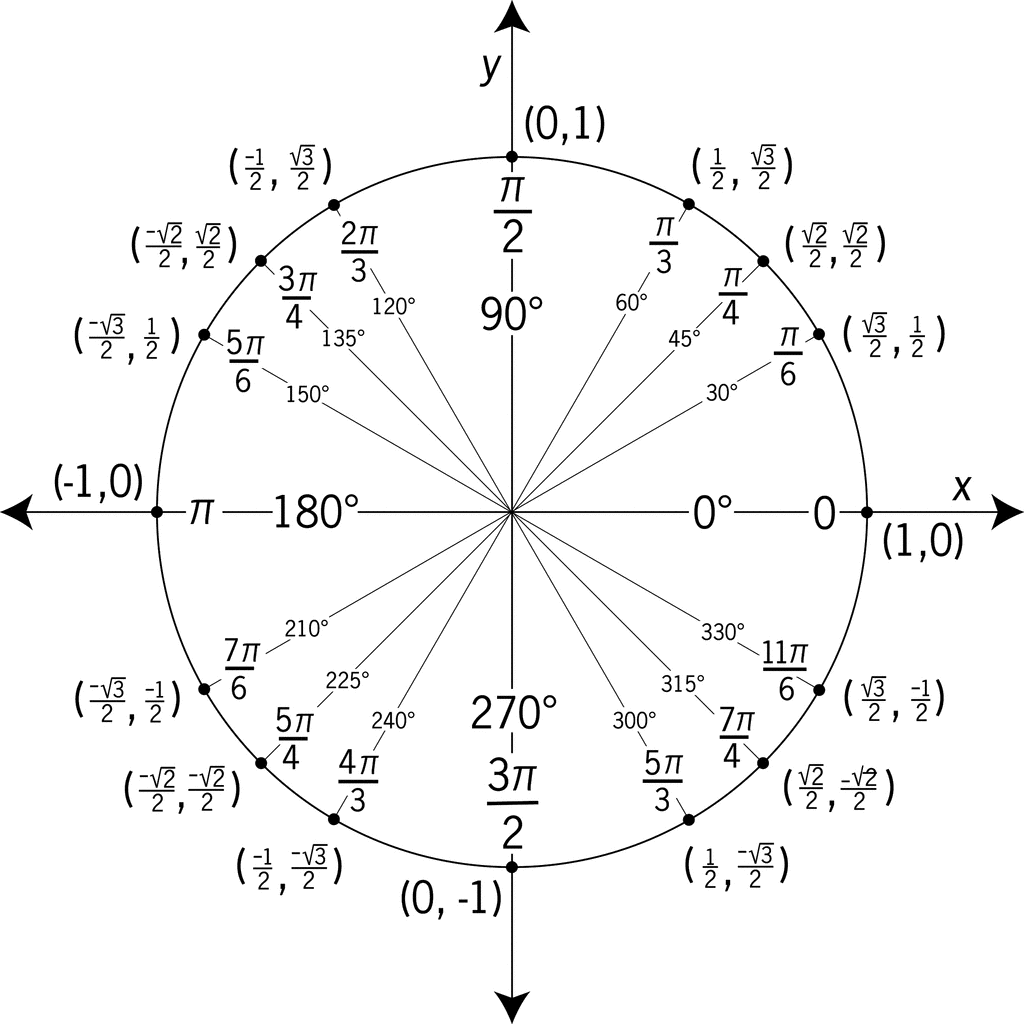
Image:

This seemingly simple table is a treasure trove of information, acting as a visual map of trigonometric values. Understanding the unit circle table is essential for anyone studying trigonometry, from high school students to aspiring engineers. It’s a key to unlocking numerous applications, from calculating the height of a building using angle measurements to designing complex circuits. This article will guide you through the mysteries of the unit circle table, revealing its secrets and showing how it can be your trusted companion in the world of trigonometry.

What is the Unit Circle?

The unit circle is a fundamental concept in trigonometry, representing a circle with a radius of one unit centered at the origin of a coordinate plane. This circle’s simplicity allows for clear visualization and calculation of trigonometric functions, especially sine and cosine. Each point on the unit circle can be uniquely defined by its angle measured from the positive x-axis and its corresponding coordinates.

The Unit Circle Table: Your Trigonometric Guide

The unit circle table is a concise representation of the values of sine, cosine, and tangent for common angles within the unit circle. It presents these angles in degrees and radians, providing an excellent reference point for trigonometric calculations.

Understanding the Basics

The unit circle is divided into four quadrants, each representing a different range of angles. The x-coordinate of a point on the circle corresponds to the cosine of the angle, while the y-coordinate represents the sine of the angle. The tangent can be calculated by dividing the sine by the cosine. Remember, the radius of the unit circle is always 1.

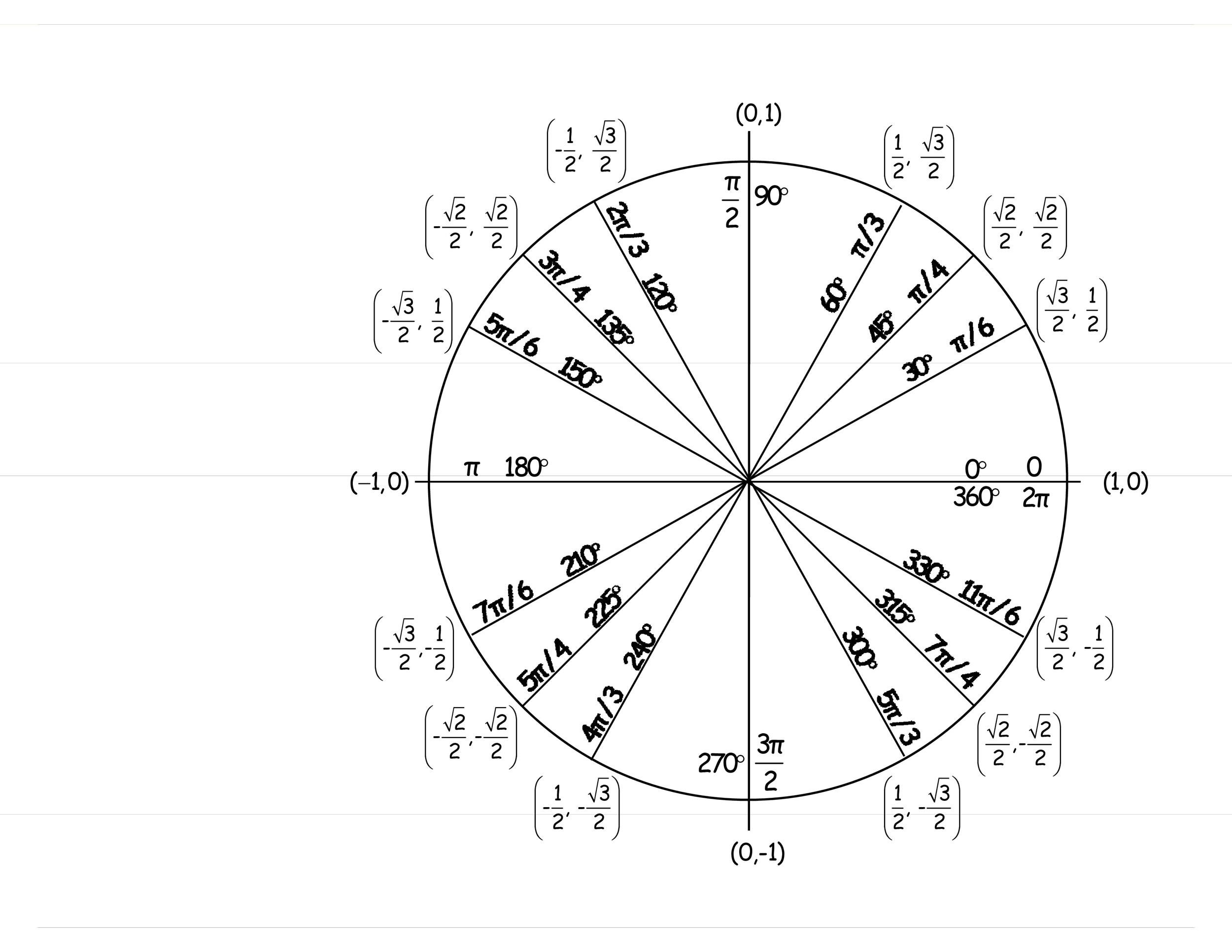
Image: templatelab.com

Key Angles and Their Values

The unit circle table emphasizes specific angles that are crucial in understanding trigonometric relationships:

• 0°, 30°, 45°, 60°, 90°: These angles form the foundation of the unit circle table. They are used to determine the values for other angles within each quadrant.
• 180°, 270°, 360°: These angles represent the boundaries between quadrants and offer essential reference points for understanding trigonometric behavior within a full cycle.

Memorizing the Values

Memorizing the trigonometric values for these key angles is key to unlocking the full potential of the unit circle table. There are various strategies for memorization, including:

• Visual aids: Creating a visual representation of the unit circle with the angle values and their corresponding coordinates can greatly enhance memorization.
• Mnemonic devices: Using mnemonics like “All Students Take Calculus” (ASTC) to remember the sign of trigonometric functions in each quadrant can be helpful.
• Practice: Consistent practice solving trigonometric problems using the unit circle table reinforces the memorization process and builds proficiency.

Applications of the Unit Circle Table

The unit circle table goes beyond being just a theoretical tool; it has diverse real-world applications in various fields:

1. Engineering:

Engineers use trigonometric functions based on the unit circle to calculate forces, stresses, and strains in structures. For instance, when designing bridges, the unit circle table helps determine the angle of cables needed to support the bridge’s weight.

2. Navigation:

Navigators rely on trigonometric calculations based on the unit circle table to determine locations, distances, and directions. This is particularly important for air and sea navigation, where accurate calculations are crucial for safety.

3. Physics:

Physics utilizes trigonometric functions for analyzing oscillations, wave motion, and electromagnetic fields. The unit circle table helps understand the relationship between displacement, amplitude, and phase in wave phenomena.

4. Computer Graphics:

Computer graphics programmers utilize trigonometric functions derived from the unit circle for creating animations and simulating realistic movements. The unit circle table helps generate smooth transitions and natural-looking motions in virtual environments.

Beyond Basic Understanding: Exploring Special Cases

The unit circle table can also be used to calculate the values of trigonometric functions for angles beyond the typical 0, 30, 45, 60, and 90 degrees. This is achievable by understanding the concept of reference angles and their relation to the unit circle:

Reference Angles

A reference angle is the acute angle formed between the terminal side of an angle and the x-axis. Using the unit circle table and knowledge of reference angles, you can find the trigonometric values for any angle.

Example:

Let’s say you need to find the sine of 150 degrees. The reference angle for 150 degrees is 30 degrees. Since sine is positive in the second quadrant, the sine of 150 degrees is the same as the sine of 30 degrees (which is 1/2).

Unit Circle Table

Conclusion

The unit circle table is an indispensable tool for mastering trigonometry. Its ability to visualize trigonometric functions and streamline calculations makes it a powerful asset in various fields. From basic understanding of trigonometric values to solving complex problems involving angles and their relationships, the unit circle table provides a clear and concise guide. As you dive deeper into the world of trigonometry, understanding and utilizing the unit circle table will be a valuable companion in your journey of discovery.

Remember, practice is key! Utilize the unit circle table, explore its applications, and don’t hesitate to experiment with different angles. The journey to mastering trigonometry is exciting, and the unit circle table is your trusted compass along the way!