What is the Percent of 1/25? A Comprehensive Guide

Imagine you’re baking a cake and the recipe calls for 1/25th of a cup of baking powder. You might naturally wonder, what percentage of the cup is that? This is a common question that arises when dealing with fractions, and it’s a fundamental concept in understanding how fractions relate to percentages. Understanding how to calculate the percentage equivalent of a fraction gives you a valuable tool for everyday situations, from cooking and budgeting to interpreting data and analyzing information.

Image: samuelthomson.z19.web.core.windows.net

In this comprehensive guide, we will delve into what exactly the percent of 1/25 is and how to calculate it. We will explore the underlying concepts of fractions and percentages, and provide practical examples to illustrate these concepts. By the end of this article, you’ll not only know the percentage of 1/25 but also comprehend the process of converting any fraction into a percentage.

Understanding Fractions and Percentages

Fractions and percentages are different ways of representing parts of a whole. A fraction expresses a part of a whole as a division of two numbers, the numerator and the denominator. For instance, 1/25 represents one out of twenty-five equal parts of a whole. A percentage, on the other hand, expresses a part of a whole as a fraction of 100, symbolized by the ‘%’ sign. It essentially tells you how many out of every hundred you have.

The key to understanding how to convert a fraction to a percentage lies in recognizing that both fractions and percentages represent parts of a whole. We can think of percentages as a specific type of fraction where the denominator is always 100. This allows us to easily convert between these two representations and gain valuable insights from both.

Converting Fractions to Percentages: The Key Formula

The process of converting a fraction to a percentage is straightforward. The core concept involves rewriting the fraction so that its denominator is 100. To achieve this, we utilize a simple formula that involves multiplying the fraction by 100%. Let’s break down the steps involved:

1. Divide the numerator by the denominator: In the case of 1/25, we divide 1 by 25, which gives us 0.04.
2. Multiply the result by 100%: We multiply 0.04 by 100% to get 4%. This signifies that 1/25 is equivalent to 4%.

Let’s illustrate this with another example. Suppose we have the fraction 3/4. Dividing the numerator (3) by the denominator (4), we obtain 0.75. Multiplying 0.75 by 100%, we get 75%, thus representing 3/4 as a percentage.

Practical Applications of Converting Fractions to Percentages

Understanding the process of converting fractions to percentages has vast practical applications in various fields. In daily life, this skill is essential for tasks like:

• Calculating discounts: When a store offers a 20% discount, it’s essentially offering a 1/5th reduction in the price. By converting the percentage discount to a fraction, you can easily calculate the actual amount saved.
• Interpreting data: Statistics and research often present data in percentages. Knowing how to convert fractions to percentages allows you to analyze and understand these data presentations effectively, gaining valuable insights for decision-making.
• Cooking and baking: Recipes sometimes use fractions to express ingredient quantities. Understanding the percentage equivalent of these fractions helps you to adjust recipes according to your needs, ensuring consistent results.

Beyond everyday life, this skill is crucial for various professional fields including finance, marketing, engineering, and medicine. Being able to effectively convert fractions to percentages allows professionals in these fields to analyze data, make informed decisions, and communicate effectively.

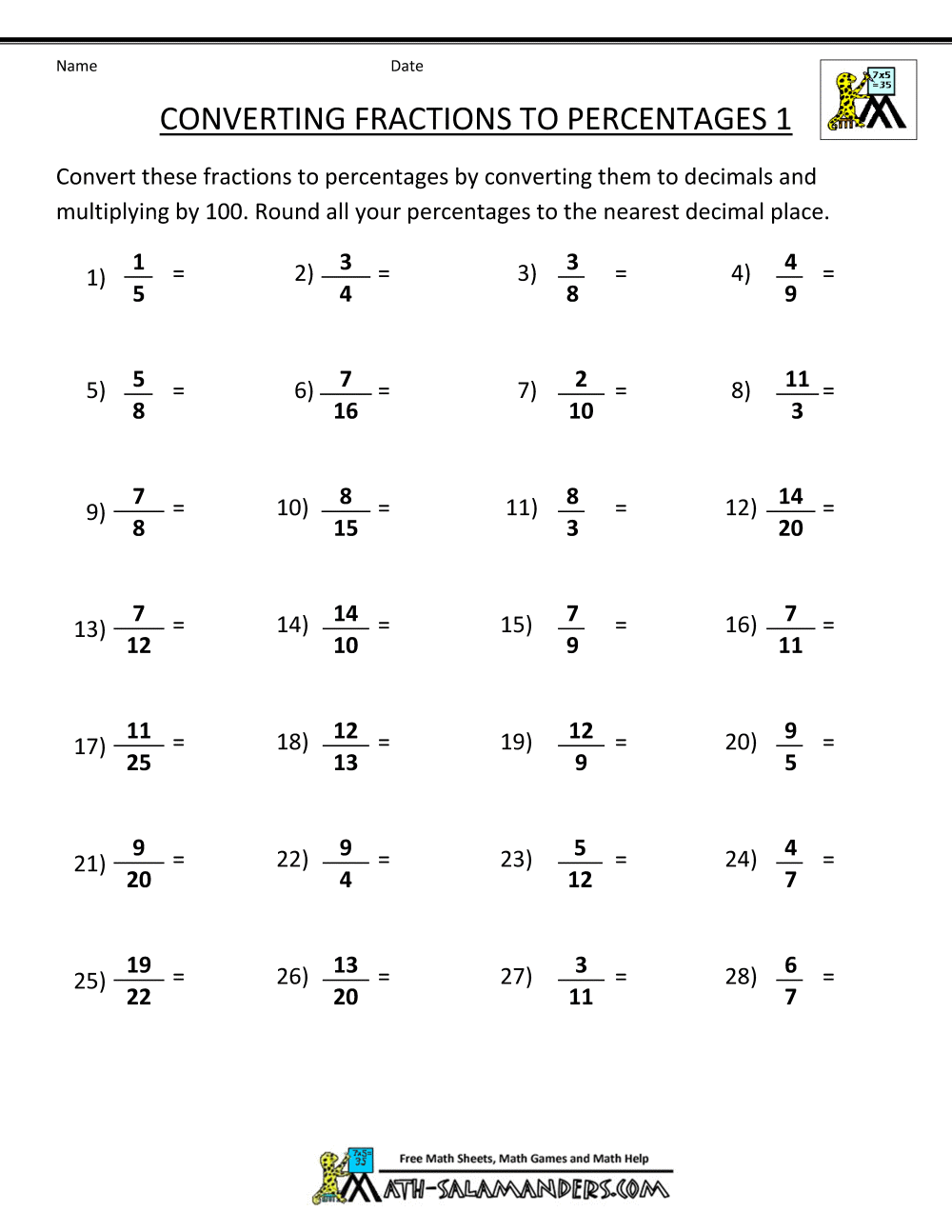
Image: classschooldisadvance.z13.web.core.windows.net

Tips and Expert Advice for Converting Fractions to Percentages

Here are some tips and expert advice to further enhance your understanding of converting fractions to percentages:

• Simplify fractions before converting: If the fraction can be simplified, do so before converting it to a percentage. This can make the calculation easier and prevent rounding errors.
• Use a calculator: For larger or more complex fractions, using a calculator can significantly speed up the conversion process. Most calculators have a dedicated percentage button (%) that simplifies the calculations.
• Practice with various examples: Converting fractions to percentages is a skill that requires practice. Working through different examples will strengthen your understanding and improve your accuracy.

Remember, converting fractions to percentages is a fundamental skill that can be applied in various situations. By practicing and utilizing the tips mentioned above, you can master this skill and navigate the world of fractions and percentages with confidence.

FAQs about Fractions and Percentages

Q: Can you convert percentages back to fractions?

Yes, you can convert percentages back to fractions. To do so, follow these steps:
1. Divide the percentage by 100.
2. Simplify the resulting fraction to its lowest terms.

For example, to convert 75% back to a fraction, divide 75 by 100 to get 0.75. Then, write 0.75 as a fraction (75/100) and simplify to 3/4.

Q: What are some practical examples of this conversion besides the ones you mentioned?

Here are some more examples:
* **Finance:** Calculating interest rates on loans or investments often requires converting fractions to percentages.
* **Statistics:** Understanding survey results or data analysis can involve converting fractions, like proportions of respondents, to percentages for easier comprehension.
* **Health & Nutrition:** Many food labels indicate nutritional information as percentages (for example, % Daily Value). Understanding these percentages requires knowing how to convert fractions.

Q: Is there an easy way to remember the formula for converting fractions to percentages?

A handy mnemonic is “To get a percent, multiply by 100!” This emphasizes the key step of multiplying the decimal form of the fraction by 100% to arrive at the equivalent percentage.

What Is The Percent Of 1/25

Conclusion

Knowing how to convert a fraction to a percentage is a valuable skill that can enhance your comprehension of various situations. Understanding the correlation between these two mathematical representations empowers you to interpret data, make informed decisions, and navigate everyday tasks with greater ease. By practicing and applying the steps and tips outlined in this article, you can confidently convert fractions to percentages and unlock a world of possibilities.

Are you interested in learning more about fractions and percentages? Share your thoughts and questions in the comments below. We would love to hear from you and continue exploring this fascinating world of numbers.