Delving into the Two-Sheet Hyperboloid – A Journey Through Geometric Wonder

Have you ever encountered a shape so unique that it seems to defy the laws of our three-dimensional world? A shape where curves twist and turn, creating a mesmerizing spectacle of intersecting lines and boundless space? This, my friends, is the realm of the two-sheet hyperboloid, a geometric marvel that has long fascinated mathematicians, scientists, and artists alike.

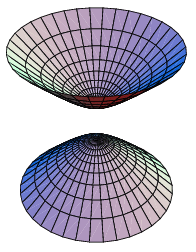
Image: mathworld.wolfram.com

But what exactly is a two-sheet hyperboloid? In essence, it’s a three-dimensional surface defined by a specific quadratic equation that results in a pair of distinct, open surfaces that resemble two infinite trumpets facing each other. This seemingly abstract concept finds surprising applications in various fields, from designing cooling towers to understanding the intricate movements of celestial bodies. This article will delve into the fascinating world of the two-sheet hyperboloid, exploring its properties, history, and real-world implications.

A Brief History: Unraveling the Two-Sheet Hyperboloid

The history of the two-sheet hyperboloid intertwines with the development of analytical geometry. In the 17th century, brilliant mathematicians like René Descartes and Pierre de Fermat introduced the concept of representing geometric objects using algebraic equations. This revolutionized the study of shapes, allowing for a more precise and systematic understanding of their properties.

The two-sheet hyperboloid, like many other geometric shapes, emerged as a result of this groundbreaking work. Early mathematicians recognized that certain quadratic equations could generate a surface that had two distinct, interconnected parts. However, the full extent of this fascinating shape’s potential was only fully appreciated with the advent of calculus and linear algebra in the 18th and 19th centuries.

Understanding the Essence: A Mathematical Perspective

To grasp the essence of the two-sheet hyperboloid, we must approach it through the lens of mathematics. The shape is defined by a quadratic equation in three variables, typically expressed as:

x²/a² – y²/b² – z²/c² = 1

Where a, b, and c are constants that determine the shape and size of the hyperboloid. This equation, when plotted in three-dimensional space, results in two distinct, open surfaces that are symmetric about the origin and extend infinitely along the x-axis.

The defining characteristic of the two-sheet hyperboloid lies in its negative coefficient for the y² and z² terms. This negative sign dictates that the y and z axes are perpendicular to the imaginary axis, resulting in the two open surfaces separated by a gap along the x-axis. This gap, known as the “throat” of the hyperboloid, is an essential feature that distinguishes it from other quadratic surfaces, such as the paraboloid and the ellipsoid.

Real-World Applications: From Cooling Towers to Cosmology

Beyond its inherent mathematical beauty, the two-sheet hyperboloid finds surprising applications in various fields. Its unique shape and geometry make it ideal for solving practical problems in engineering, architecture, and even cosmology.

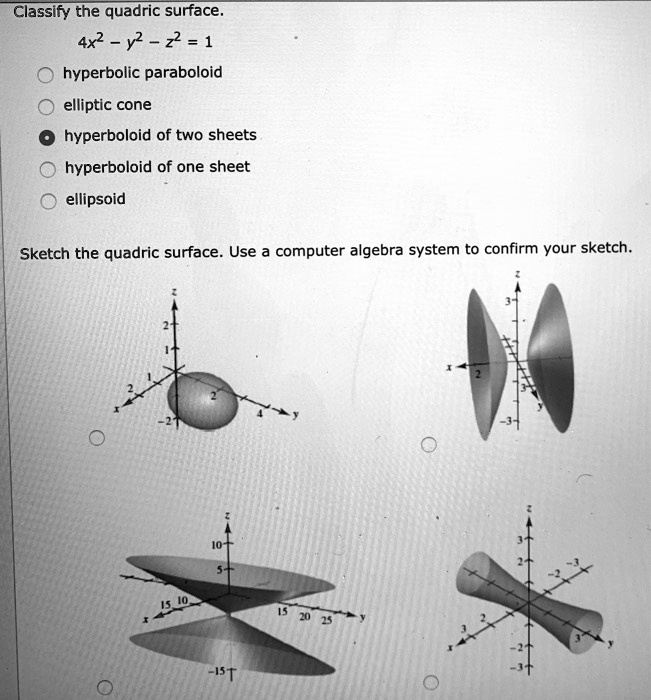
Image: www.numerade.com

Engineering Marvels: Cooling Towers

One of the most recognizable applications of the two-sheet hyperboloid is in the design of cooling towers for power plants. The shape’s open structure allows for efficient airflow and heat dissipation, ensuring proper cooling of the plant’s turbines and machinery. The two-sheet hyperboloid’s unique geometry optimizes this process by minimizing air resistance and maximizing the surface area exposed to the environment.

Architectural Innovations: Hyperbolic Paraboloids

The two-sheet hyperboloid’s close relative, the hyperbolic paraboloid, has found its place in architecture as a striking and functional building element. The hyperbolic paraboloid is a ruled surface, meaning it can be created by straight lines. This property makes it ideal for constructing roofs, shells, and other structures with minimal material and elegant aesthetics. The Sydney Opera House and the St. Louis Gateway Arch are famous examples of hyperbolic paraboloids being used to create architectural masterpieces.

Cosmic Mysteries: Black Holes and Gravitational Lensing

While the two-sheet hyperboloid appears in the realm of engineering and architecture, it also holds a place in the study of the cosmos. Theoretical physicists utilize this shape to model the gravitational field around black holes. The extreme gravity of a black hole warps the surrounding spacetime, creating a region of infinite curvature known as the event horizon. This distorted spacetime can be represented as a two-sheet hyperboloid, with the throat marking the boundary beyond which even light cannot escape.

Furthermore, the two-sheet hyperboloid plays a role in understanding gravitational lensing, a phenomenon where the gravity of massive objects like galaxies or black holes bends the path of light, causing distorted images of distant objects. The lensing effect can be modeled using the two-sheet hyperboloid, providing valuable insights into the distribution of matter in the universe.

Two Sheet Hyperboloid

Exploring Further: The Endless Possibilities

The two-sheet hyperboloid, with its unique geometry and diverse applications, offers a glimpse into the fascinating world of mathematics and its profound connection to the physical world. While this article has only touched upon a few of this shape’s facets, it opens up a vast realm of exploration for those seeking a deeper understanding of its intricacies.

If you’re captivated by the beauty and elegance of the two-sheet hyperboloid, I encourage you to delve further into its mathematical foundations, explore its countless real-world applications, and appreciate the role it plays in unlocking the mysteries of the universe. From engineering marvels to cosmic wonders, the two-sheet hyperboloid stands as a testament to the power and beauty of geometric shapes.