63 as a Fraction – Unveiling the Nuances of Whole Numbers and Fractions

Have you ever wondered how a whole number like 63 can be represented as a fraction? It seems counterintuitive at first, but understanding this concept unlocks a deeper understanding of the relationship between whole numbers and fractions. In this article, we’ll explore the intricacies of representing 63 as a fraction, revealing the hidden power and flexibility of this mathematical concept.

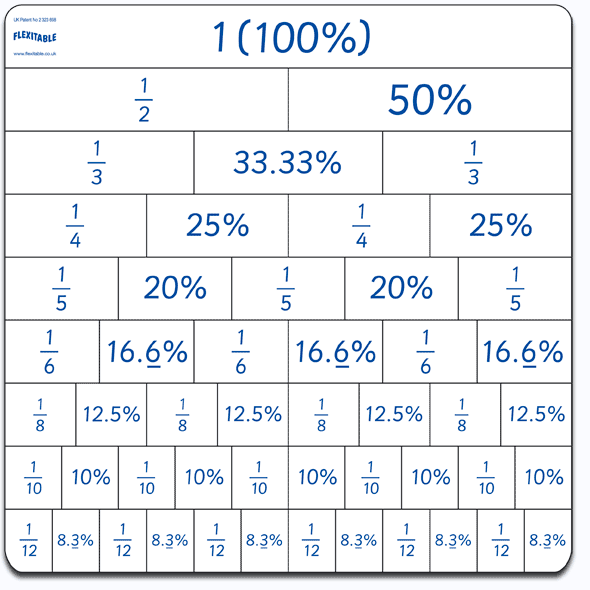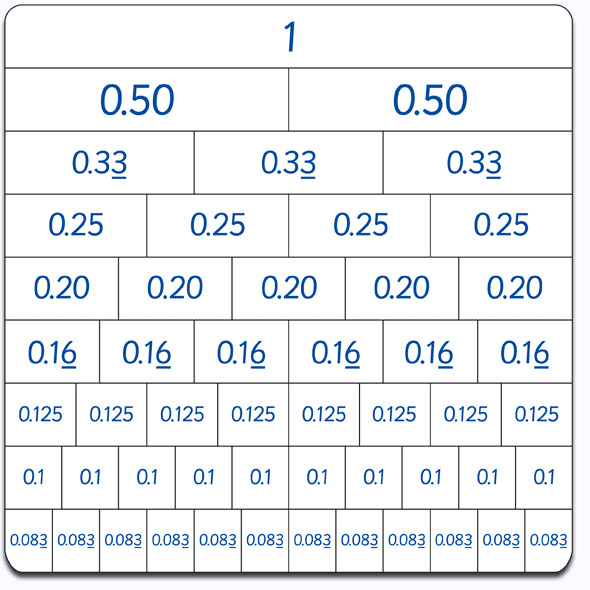
Image: flexitable.shop

Imagine you’re baking a cake and the recipe calls for 63 pieces of chocolate chips. You realize you only have bags containing 10 chips each. How many bags do you need? This simple scenario highlights the importance of understanding how to express whole numbers as fractions – it allows us to make calculations and solve real-world problems more efficiently.

The Foundation: Understanding Fractions

Before we dive into representing 63 as a fraction, let’s revisit the basic concept of fractions. A fraction represents a part of a whole, expressed as a ratio of two numbers, the numerator and the denominator. The numerator indicates the number of parts we are considering, while the denominator represents the total number of equal parts that make up the whole.

Expressing 63 as a Fraction: A Simple Approach

The most straightforward way to express 63 as a fraction is to use 1 as the denominator. This is because any number divided by 1 is itself. Therefore, 63 can be represented as:

• 63/1

This fraction indicates that we have 63 parts out of a total of 1 part, which essentially represents the whole number 63.

Exploring Equivalent Fractions: Expanding the Possibilities

While 63/1 is a valid representation, it’s not the only way to represent 63 as a fraction. We can create equivalent fractions by multiplying both the numerator and the denominator by the same number. For instance:

• 63/1 x 2/2 = 126/2
• 63/1 x 5/5 = 315/5
• 63/1 x 10/10 = 630/10

These fractions are all equivalent to 63/1, meaning they represent the same value. The choice of which equivalent fraction to use depends on the context of the problem. For example, if you are working with a recipe that requires ingredients measured in halves or fifths, using one of the equivalent fractions may be more practical.

Image: www.pinterest.com

The Importance of Simplifying Fractions: Finding the Simplest Form

While equivalent fractions represent the same value, it’s often beneficial to express a fraction in its simplest form. A simplified fraction is one where the numerator and denominator have no common factors other than 1. To simplify a fraction, we find the greatest common factor (GCD) of the numerator and denominator and divide both by it.

For example, 126/2 can be simplified by dividing both numerator and denominator by 2, resulting in 63/1. This is considered the simplest form of the fraction. Simplifying fractions makes them easier to understand and compare.

Real-World Applications: Fractions in Everyday Life

Representing whole numbers as fractions has numerous real-world applications, ranging from everyday tasks to advanced scientific calculations. Let’s explore some examples:

• Cooking: Recipes often use fractions to indicate quantities of ingredients. For example, a recipe might call for 3/4 cup of flour or 1/2 teaspoon of baking soda. Understanding how to represent whole numbers as fractions allows you to easily adjust recipes based on your needs.
• Measurement: In various fields, from construction to engineering, precise measurements are crucial. Fractions are used extensively in measurement systems, allowing for greater accuracy and detail compared to using only whole numbers.
• Finance: Fractions are used in financial calculations, such as calculating interest rates, returns on investment, and debt-to-equity ratios. Understanding how to represent whole numbers as fractions allows for a more precise and nuanced analysis of financial data.

Beyond the Basics: Fractions in Advanced Mathematics

While we’ve explored basic concepts of representing whole numbers as fractions, the applications of fractions extend far beyond simple calculations. Fractions play a vital role in advanced mathematics, particularly in:

• Algebra: Fractions are used to solve equations, represent variables, and express relationships between quantities.
• Calculus: Calculus involves working with rates of change and areas under curves, often represented using fractions and their derivatives.
• Number Theory: This branch of mathematics delves into the properties of numbers, including fractions and their interactions.

63 As A Fraction

The Power of Fractions: Embracing the Versatility of Mathematics

Understanding how to represent whole numbers as fractions unlocks a world of mathematical possibilities. It allows us to work with parts of wholes, express quantities with greater precision, and navigate complex mathematical concepts. From everyday tasks to advanced scientific calculations, fractions provide a powerful tool for understanding and representing the world around us. So, the next time you encounter a whole number, consider its fractional representation and explore the hidden beauty and versatility of this fundamental mathematical concept.

This article has just grazed the surface of this rich and fascinating topic. We encourage you to delve deeper into the world of fractions by reading books, taking online courses, or exploring mathematical resources. By expanding your knowledge of fractions, you’ll unlock a deeper understanding of mathematics and its boundless applications in our world.