Factorization of 135 – A Comprehensive Guide

Have you ever wondered how to break down a number into its smaller building blocks? It’s like taking apart a Lego structure to see what pieces make it up. This process of finding the factors of a number is called factorization, and it’s a fundamental concept in mathematics. Today, we’ll dive into the fascinating world of factorization, using the number 135 as our guide. While it might seem like a simple number, 135 holds a surprising amount of mathematical depth.

Image: www.youtube.com

As a kid, I remember being captivated by the magic of numbers. Watching my teacher break down 12 into 2 x 2 x 3 felt like uncovering a secret code. I realized then that numbers weren’t just abstract symbols; they were interconnected puzzles, waiting to be unraveled. Our journey into the factorization of 135 will be just as exciting, revealing the hidden relationships within this seemingly ordinary number.

Understanding Factorization: Breaking Down Numbers

Factorization is like a mathematical detective game. We’re given a number, and our goal is to find all the numbers that divide evenly into it. These numbers we find are called the factors of the original number. Think of it like finding all the pieces that can fit together to form a specific shape – the shape being our original number, and the pieces being its factors.

For example, if we have the number 12, its factors are 1, 2, 3, 4, 6, and 12. Each of these numbers divides evenly into 12, leaving no remainder. Finding the factors of a number can be helpful in various mathematical concepts, like simplifying fractions, finding common denominators, and even solving algebraic equations.

The Factorization of 135: Discovering the Pieces

Let’s take the number 135 and break it down. The first step is to find its smallest factor, which is always 1. Then, we need to look for other numbers that divide evenly into 135. One way to do this is by systematically trying out different numbers.

We know 135 is an odd number, so it’s not divisible by 2. However, it is divisible by 3, since the sum of its digits (1 + 3 + 5 = 9) is divisible by 3. So, 135 divided by 3 equals 45.

Now, we can continue factoring 45. Again, it’s divisible by 3, giving us 15. We can factor 15 further, yielding 3 x 5. Finally, we have broken down 135 into its prime factors: 3 x 3 x 3 x 5. This means that 1, 3, 5, 9, 15, 27, 45, and 135 are all factors of 135.

Prime Factorization: The Foundation

The prime factorization of a number is a special kind of factorization where only prime numbers are used. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (like 2, 3, 5, 7, 11, etc.). Therefore, the prime factorization of 135 is 3 x 3 x 3 x 5, with 3 being a repeated prime factor. Prime factorization is extremely important in mathematics, providing the building blocks for many other mathematical concepts.

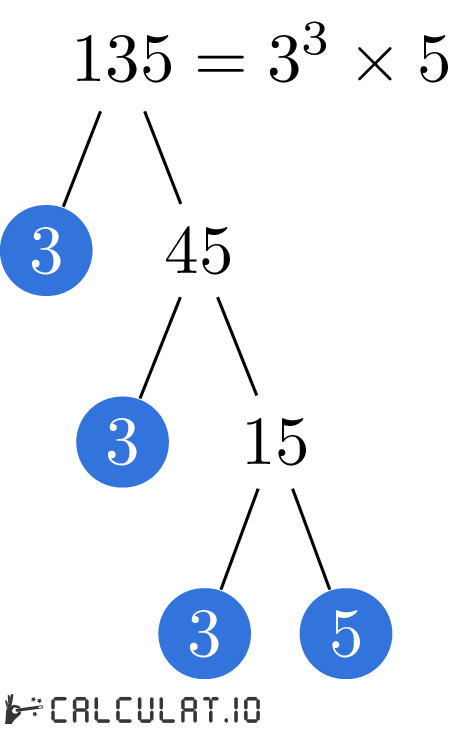
Image: calculat.io

Methods for Finding Factors: Exploring Strategies

Besides systematically checking each number, there are other methods for finding factors. One popular method is called the “factor tree.” In this method, you start with the original number and branch out, dividing it by its factors until you reach all prime factors. For example, the factor tree for 135 would be:

“`
135
/ \
3 45
/ \ / \
3 15 3 15
/ \ / \
3 5 3 5
“`

Another method is using the “division method.” Here, you repeatedly divide the original number by its prime factors, keeping track of the factors used. For 135, this would look like:

“`
3 | 135
3 | 45
3 | 15
5 | 5
| 1
“`

This leaves us with the prime factors, 3 x 3 x 3 x 5. Both methods are effective in finding the prime factors of a number.

Applications of Factorization

Beyond their theoretical significance, factorization has various practical applications in our daily lives. They are useful in simplifying fractions, finding the least common multiple (LCM) and the greatest common divisor (GCD) of two numbers, solving algebraic equations, and even in cryptography.

For example, when simplifying fractions, we can use factorization to find common factors in the numerator and denominator, allowing us to cancel them out and get a simplified fraction. The same principle applies when finding the LCM and GCD of two numbers, essential for calculations in various fields like music, architecture, and engineering. The connection between factorization and cryptography is fascinating, as the process of breaking down large composite numbers into their prime factors forms the basis for many encryption algorithms that keep our online data secure.

Tips and Expert Advice for Successful Factorization

Mastering factorization can open up a whole new world of mathematical understanding. Here are some tips from my experience that might help you achieve better success with factorization:

1) Start with the smallest prime factors: Begin by checking for divisibility by 2, 3, 5, 7, and so on. This will help you efficiently find the prime factorization of the number.

2) Utilize divisibility rules: These rules can save you time and make finding factors easier. For example, a number is divisible by 3 if the sum of its digits is divisible by 3, and a number is divisible by 5 if its last digit is a 0 or a 5. These shortcuts can greatly simplify the process.

3) Practice, practice, practice: Like any skill, factorization takes practice to master. Work through various examples, use different methods, and challenge yourself with larger numbers. This will build your confidence and fluency.

FAQs About Factorization

Q. What is the difference between factorization and prime factorization?

A. While both involve breaking down a number into smaller numbers, factorization includes all factors, both prime and composite. Prime factorization, on the other hand, uses only prime numbers.

Q. How can I tell if a number is prime?

A. A number is prime if it is greater than 1 and has only two factors: 1 and itself. For example, 7 is a prime number because its only factors are 1 and 7.

Q. What is the importance of factorization in real life?

A. Factorization plays a crucial role in many fields, including cryptography, computer science, and data analysis. It’s also fundamental to simplifying fractions, finding common denominators, and solving various mathematical problems.

Factorization Of 135

Conclusion

We’ve explored the fascinating world of factorization, using 135 as our example. From understanding the core concepts of factorization and prime factorization to exploring various methods for finding factors and their applications, this journey revealed how seemingly simple numbers hold a wealth of mathematical depth.

Now that you know more about factorization, are you ready to explore other numbers and unlock their hidden mathematical treasures?