Navigating the Washers and Disks – Mastering the Art of Volume Calculation

Imagine yourself standing before a magnificent sculpture, its curves and contours inviting you to unravel its secrets. Now imagine that you need to precisely calculate its volume, the very essence of its presence. This is where the magic of calculus comes into play, and specifically, the washer and disk methods step onto the stage.

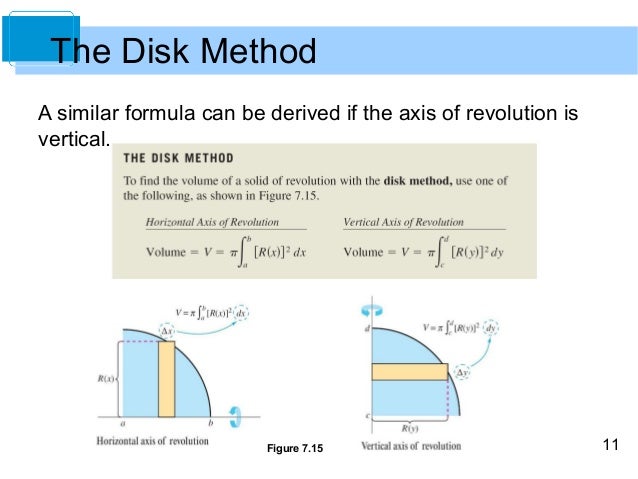
Image: sites.google.com

These methods, pillars of calculus, help us calculate volumes of complex shapes by slicing them into infinitesimally thin cross-sections. Whether it’s a solid of revolution, formed by rotating a shape around an axis, or a shape with intricate boundaries, the washer and disk methods provide a systematic approach to unraveling these volumetric mysteries. But how do you choose the right method for the task at hand? Let’s embark on a journey to understand the nuances of these powerful tools.

Understanding the Fundamentals: Discs and Washers

The Disk Method: Simplicity at its Best

The disk method is akin to stacking a stack of coins. It’s used when the region being rotated has no void or hollow space. Think of a circle being rotated around its diameter to form a sphere. Here’s the process in a nutshell:

• Slice: Divide the region into infinitesimally thin slices perpendicular to the axis of rotation.
• Rotate: Each slice, when rotated, forms a solid disk.
• Integrate: The volume of the solid is obtained by integrating the area of each disk over the entire range of the shape.

The formula that captures this process is:
$$V = \int_a^b \pi [f(x)]^2 dx$$

Where:

• V represents the volume.
• a and b are the limits of integration along the x-axis.
• f(x) is the function defining the shape being rotated.
• dx represents the infinitesimal width of each slice.

The Washer Method: Accounting for the Hole

Now, imagine a doughnut, with a hole in the center. This is where the washer method comes into play. This method is used when the region being rotated has a void, creating a hole in the solid. Let’s imagine a circle with an inner hole being rotated around its axis.

• Slice: Again, we slice the region into thin slices, but this time, the slices are shaped like washers – with an outer radius and an inner radius.
• Rotate: When rotated, each slice creates a washer-like solid.
• Integrate: The volume is calculated by integrating the difference between the outer area and inner area of each washer over the entire range of the shape.

The formula for the washer method captures this concept:
$$V = \int_a^b \pi [f(x)]^2 – \pi [g(x)]^2 dx$$

Where:

• V represents the volume.
• a and b are the limits of integration along the x-axis.
• f(x) defines the outer radius of the washer.
• g(x) defines the inner radius of the washer.
• dx represents the infinitesimal width of each washer.

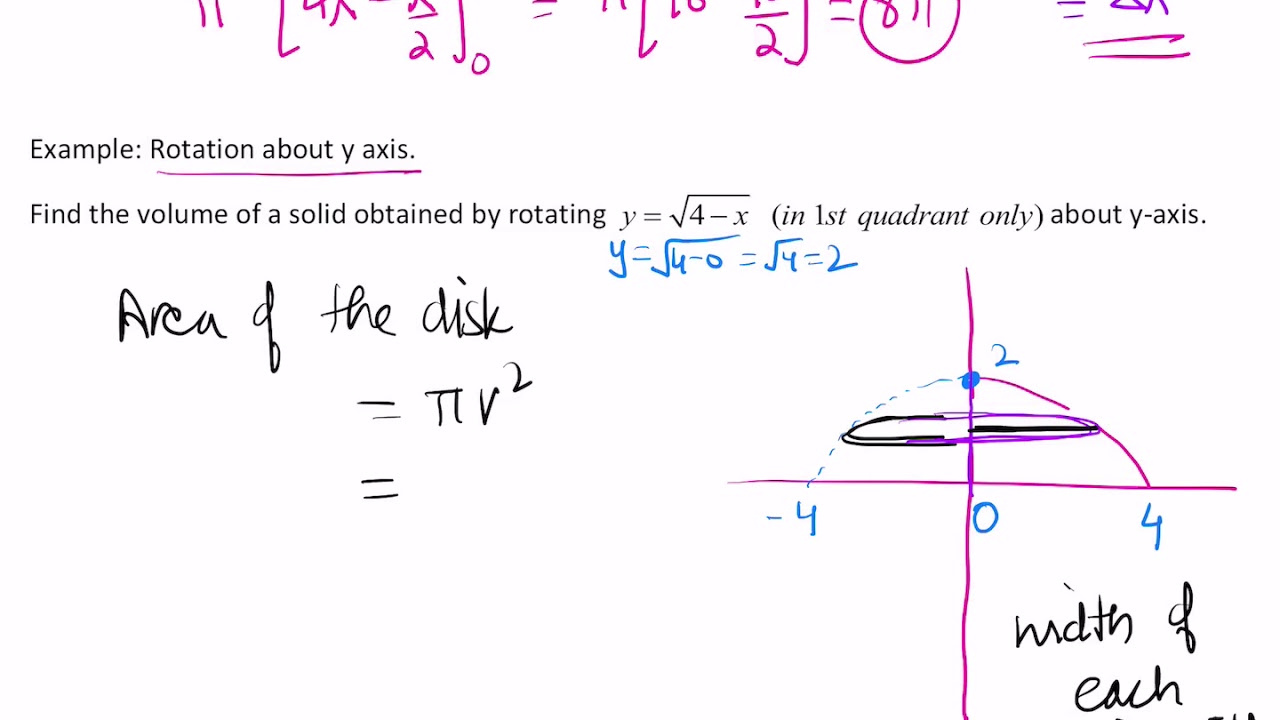
Image: www.youtube.com

Choosing the Right Method: A Guide to Success

The choice between the disk and washer method depends on the geometry of the shape being rotated. Here’s a simple breakdown:

• Disk method: Use the disk method when the region being rotated has no void, i.e., no holes.
• Washer method: Use the washer method when the region being rotated has a void, creating a hole in the solid.

The key lies in visualizing the shape and understanding if the slicing results in a simple disk or a washer with an inner and outer radius.

For instance, if we rotate the region bounded by the curve y = x^2 and the x-axis about the x-axis, we use the disk method. However, if we rotate the region bounded by the curves y = x^2 and y = x about the x-axis, we use the washer method because there is a void between the two curves.

Real-World Applications: Where Washers and Disks Shine

Beyond the realm of textbooks, the washer and disk methods find practical applications in various fields:

• Engineering: Calculating volumes of tanks, pipes, and other complex structures. These calculations are crucial in designing and constructing efficient and reliable infrastructure.
• Architecture: Estimating the volume of materials required for building projects. Architects and engineers utilize these methods to ensure cost-effective and structurally sound constructions.
• Physics: Calculating the moment of inertia of objects. This parameter is vital for understanding how objects rotate and how forces affect their motion.
• Medicine: Analyzing the volume of organs and tissues for diagnostic purposes. This is particularly relevant in imaging techniques and medical research.

Example Scenarios: Putting the Methods into Action

Let’s delve into concrete examples to solidify our understanding of the washer and disk methods:

Example 1: A Solid of Revolution

Imagine a region bounded by the curve y = x^2, the x-axis, and the line x = 2. We want to calculate the volume of the solid generated when this region is rotated about the x-axis. This shape resembles a bowl, and we can use the disk method.

1. Slice: We slice the region into thin vertical slices perpendicular to the x-axis, each slice being a thin rectangle.

2. Rotate: When each slice is rotated about the x-axis, it forms a disk with a radius of f(x) = x^2.

3. Integrate: To find the volume, we integrate the area of each disk over the range of x from 0 to 2. This gives us:
$$V= \int_0^2 \pi [x^2]^2 dx = \int_0^2 \pi x^4 dx = \left[\frac\pi x^55\right]_0^2 = \frac32\pi5$$

Example 2: A Washer with a Twist

Let’s visualize a region bounded by the curves y = x^2 and y = x, being rotated around the x-axis. This forms a solid with a hollow center, resembling a donut. Here, we employ the washer method.

1. Slice: Again, we slice the region into thin vertical slices. But this time, each slice forms a washer with an outer radius of f(x) = x and an inner radius of g(x) = x^2.

2. Rotate: Rotating each washer about the x-axis creates a washer-shaped solid.

3. Integrate: Finally, we integrate the difference between the outer and inner areas of each washer over the range of x from 0 to 1. This calculation yields:
$$V = \int_0^1 \pi [x]^2 – \pi [x^2]^2 dx = \int_0^1 \pi (x^2 – x^4) dx = \left[\pi\left(\fracx^33 – \fracx^55\right)\right]_0^1 = \frac2\pi15$$

Beyond the Basics: Exploring Advanced Concepts

While the disk and washer methods are robust tools, calculus offers a plethora of other techniques for calculating volumes. Some notable concepts include:

• Shell method: This method involves slicing the region into cylindrical shells parallel to the axis of rotation. This method is particularly useful when integrating with respect to the other variable (y in this case) and the washer method becomes complex.
• Double and triple integrals: These powerful techniques allow for calculating volumes of more complex shapes with multiple dimensions.

Washer Vs Disk Method

Conclusion: Mastering the Art of Volume Calculation

The washer and disk methods are invaluable tools for understanding and calculating volumes of revolution. These methods, rooted in the principles of calculus, offer a systematic approach for unraveling the intricate geometry of solids. From engineering to architecture, physics, and beyond, these methods have a profound impact on our understanding and manipulation of the world around us. So, the next time you encounter a complex shape, remember the washer and disk methods and embrace the power of calculus to solve those volumetric puzzles.